휘트스톤 브리지
휘트스톤 브리지는 미지저항값을 결정하는데 사용하는 회로이다 일반적인 휘트스톤 브리지는 아래 그림 처럼 생겼다.
4개의 저항이 다이아몬드와 같은 배열로 구성되어 있음을 볼 수 있다. 보통 이런 배열로 휘트스톤 브리지를 그린다
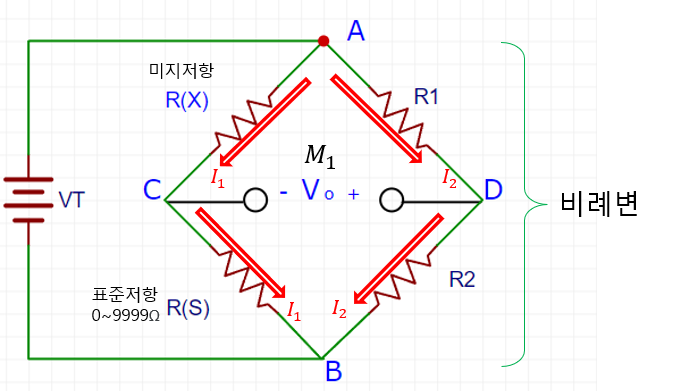
위그림을 보면 인가전압 VT가 단자 A 와 B 에 연결되는데, 이는 휘트스톤 브리지의 입력단자 나타낸다. 검류계 M1이 출력단자인 C와 D 사이에 연결되는데 이 M1은 0눈금이 가운데 위치하며 전류의 흐름에 아주 민감하게 반응하는 전류계이다.
그림에 보인 것처럼 미지저항 RX는 가변 표준저항RS와 같은 가지에 위치하고 있다. 표준저항 RS가 0~9999 Ω 사이에서 1Ω 단위로 변하는 매우 정밀한 저항이다 R1과 R2 는 비례변(RATIO ARM) 으로 다른 가지를 구성하고 있다 R1와 R2 또한 이상적인 정밀저항으로 저항오차가 아주작다. 이제 미지저항 RX 의 값을 구하기위해 표준저항 RS를 조정하여 M1에서 전류가 정확히 0이 되게 한다 이렇게 0이 되었을때 휘트스톤 브리지는 평형을 이루었다고 한다. 이렇게 M1에 전류가 흐르지 않으면 RX와 RS 사이의 전압분배는 비례변의 저항R1과 저항 R2 사이의 전압분배와 같게 된다.
즉 RX- RS 가지의 전압분배가 R1-R2가지의 전압분배와 같다는것은 C 와 D 사이의 전위치가 0V이라는 것을 말해준다
평형 상태에서 등가 전압비는 다음과 같이 나타낼수 있다.
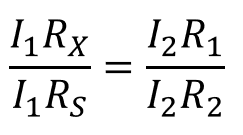
I1과 I2은 식에서 상쇄됨으로
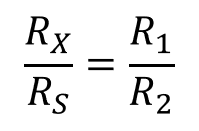
RX에 대해서 풀면 다음 결과를 얻는다.
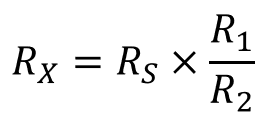
비례변(RATIO ARM) R1/R2는 대부분의 경우에 그값이 변할수 있는데 보통 100/1 ,10/1,1/1,1/10,1/100 등의 10급수로 변하게된다 그러나 RS 표준저항을 조정하면 여전히 브리짓가 평형을 이루게된다 즉 RX의 측정 정밀도는 R1/R2의 비에 따라 결정된다 만약 1/10비면 오차는 0.1Ω 이내고 1/100이라면 0.01Ω 이내 정밀도를 갖고 있따 . 또한 R1/R2의 비는 측정할수 있는 미지저항의 최대값을 결정한다.
'공학 > 전기' 카테고리의 다른 글
| GROB's basic electronics 회로 이론-6.전압분배기와 전류분배기(전류분배기) (0) | 2022.07.10 |
|---|---|
| GROB's basic electronics 회로 이론-6.전압분배기와 전류분배기(직렬전압분배기) (1) | 2022.07.05 |
| GROB's basic electronics 회로 이론-5.직병렬회로(미지값이 들어간 회로 해석) (0) | 2022.06.27 |
| GROB's basic electronics 회로 이론-5.직병렬회로( 직병렬로 연결된 저항 뱅크와 저항열의 회로 해석) (0) | 2022.06.22 |
| GROB's basic electronics 회로 이론-5.직병렬회로(직렬로 연결된 저항뱅크) (0) | 2022.06.20 |