1.가지전류법
키르히호프의 전압 법칙을 사용하여 아래 그림의 회로를 분석할 수 있다. 세 저항대 대한 전류와 전압을 구해보자.
먼저 전류 방향을 나타내고 가정한 전류 방향에 맞도록 각저항에 걸리는 전압의 극성을 표시한다. 저항을 흐르는 전류는 전류가 들어가는 곳을 +로 만든다 아래 그림에서 전원 V1은 전류가 R1을 통해서 왼쪽에서 오른쪽으로 흐르도록 하고 V2는 R2를 통해 오른쪽에서 왼쪽으로 흐르게 한다

R1, R2, R3를 각각 흐르는 I1 I2 I3으로 표시할 때 이 3개의 미지 전류를 구하기 위해서는 3개의 방정식이 필요하다 키르히호프의 전류 법칙으로부터 C점으로 들어오는 전류는 나가는 전류의 합과 같기에 I1+I2=I3식을 얻는다. 그러므로 R3을 흐르는 전류는 I1+I2로 구할 수 있다.
두 미지 전류 I1과 I2를 구하기 위해서는 2개의 독립 방정식이 필요하다 이방 정식들은 2개의 루프 주위에 두 개의 키르히호프 전압 방정식을 세워서 얻는다 위 그림에는 안쪽 루프 2개 바깥쪽 루프 1개 모두 3개의 루프지만 필요한 건 2개뿐이라 안쪽 루프만 이용한다
1-2. 루프 방정식
V1을 포함한 루프에서 B점부터 시작하여 시계방향으로 V1, V(R1), V(R3)을 일주한다. 이 루프 방정식은

V2를 포함한 루프에서 F점부터 시작하여 반시계 방향으로 V2, V(R2), V(R3)을 일주한다. 이 루프 방정식 2는

전압강하들을 구하기 위해 R1, R2, R3의 값을 구하면

이 값을 위 V1 루프 방정식에 대입하면

루프 2에 대입하면

6(I1+I2)을 정리하고 이항 하면 두 루프 방정식은 다음과 같이 정리된다.


이제 위쪽 방정식을 6으로 나누고 아래 방정식을 3으로 나누어 식을 간단하게 하면


1-3. 전류에 대한 풀이
두 미지 전류 I1과 I2에 대한 이 2개의 방정식을 풀어 회로망의 답을 구할 수 있다. 이 식들이 회로의 모든 저항을 포함하고 있다는 사실을 주목해야 한다. 전류 I1과 I2는 연립방정식을 풀기 위한 여러 가지 방법을 적용하여 계산할 수 있다 변수 소거법을 사용한다면 위식에 3을 곱해 I2항이 같게 만든 그러면


I2를 소거하면


이 5A의 I1이 R1을 흐르는 전류다. 그 방향은 I1의 결과가 (+)이므로 앞에서 가정한 것과 같이 A->C로 흐른다. I2는 두 루프 방정 식중 하나에 I1 대신 5를 대입하여 계산한다. 아래식에 대입을 하면

I2의 (-) 부호는 전류가 가정한 방향과 반대로 흐른다는 것을 의미한다. 그러므로 I2는 앞에서 가정한 것처럼 E->C 가아니라 C->E로 R2를 통해 흐른다
I2의 결과가 (-)인 이유
위 그림에서 I2는 V2가 E-> C방향으로 전류를 흘리기 때문에 R2를 통해 이 방향으로 흐른다고 가정한다. 그러나 다른 전압원 V1은 C에서 E로 R2를 통해 다른 V2와 다른 방향으로 전류를 흘리고 있다. I2의 결과가 -1A인 것은 V1에 의해 R2를 흐르는 전류가 V2에 의 한 전류보다 크다는 것을 의미한다 그렇기에 실제 결과는 C->E로 R2를 통해 1A가 흐르게 된다
I2의 실제 방향을 아래 그림에 보였는데 이 회로에는 모든 결과 값들이 표시되어 있다. V(R2) 극성이 맨 처음 그림에서 가정한 극성과 반대가 되어있음에 주의해야 한다 R2를 흐르는 순 전류는 실제 C->E로 흐르기 때문에 C에 연결된 R2의 끝부분이 (+)이다. 그렇지만 V2의 극성은 그 자신이 극성을 발생시키는 전압원이기 때문에 두 회로에서 동일하다

R3에 흐르는 I3를 계산해보면

4A의 I3은 C->D로 가정한 방향과 같다 비록 I2의 부호가 단지 방향이 반대인 것을 의미하지만 가정한 방향에 대해 세워진 대수식을 대입할 때는 -1의 대수 값을 사용해야 한다.
1-4. 전압 계산
앞에서 구한 모든 전류값으로 각 저항에 걸리는 전압을 다음과 같이 계산할 수 있다.
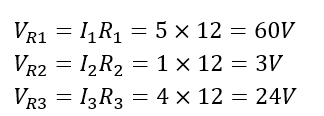
전압을 계산하기 위해 모든 전류는 흐르는 방향대로 적용하여 +로 정했다 각전 압강 하의 극성은 전류의 실제 방향에 따라 정해지는데 전류가 들어가는 곳을 +로 하였다. 루프 2에서 V(R2)와 V(R3)이 반대 극성인 것에 주의하라. 그때 -3V와 +24V의 합은 V2인 +21V와 같다.
결과 검산
C점에서 : 5A=4A+1A
D점에서 : 4A+1A=5A
B점으로부터 시계방향으로 V1을 포함한 루프에서,
-84V+60V+24V=0
F점으로부터 반시계 방향으로 V2를 포함한 루프에서
-21V-3V+24V=0
직렬회로나 병렬회로에 대한 어떤 특정한 공식을 적용하지 않고 오직 키르히호프의 두 법칙과 옴의 법칙만을 사용하여 회로를 해석한 것에 주목해야 한다 어떤 회로든지 키르히호프의 법칙들을 루프 둘레의 전압들과 한 가지점에서의 전류들에 대해 적용하여 해석할 수 있다.
'공학 > 전기' 카테고리의 다른 글
| GROB's basic electronics 회로 이론-7.키르히호프법칙(망전류법) (0) | 2022.08.03 |
|---|---|
| GROB's basic electronics 회로 이론-7.키르히호프법칙(절점전압법) (0) | 2022.08.02 |
| GROB's basic electronics 회로 이론-7.키르히호프법칙(키르히호프의 전압 법칙,루프방정식) (0) | 2022.07.13 |
| GROB's basic electronics 회로 이론-7.키르히호프법칙(키르히호프법칙의전류법칙,전류방정식) (0) | 2022.07.12 |
| GROB's basic electronics 회로 이론-6.전압분배기와 전류분배기(전류분배기) (0) | 2022.07.10 |