노턴 정리
노턴 정리는 전압 대신 전류의 항으로 회로를 단순화하는 데 사용된다. 많은 경우에 있어 전류의 분배에 대한 해석은 전압으로 해석하는 것보다 쉬울 수 있다. 그러므로 전류 분석을 위해서 노턴 정리를 사용하여 회로망을 전류원을 가진 간단한 병렬회로로 줄일 수 있다. 전류원에 대한 개념은 직렬 부품에 나누어지는 전체 전압을 공급하는 전압원에 대응되는 것으로 전류원은 병렬 가지들에 나누어 흐르게 되는 전체 전류를 공급한다.
노턴 등가 회로
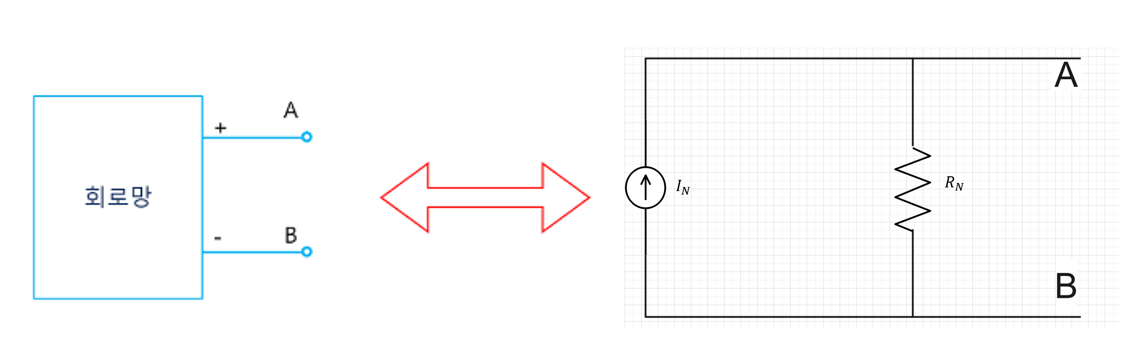
위 회로 그림처럼 노턴 정리는 단자 A와 B에 연결된 전체 회로망이 저항 R(N) 1개와 병렬인 전류원 I(N) 1개로 대치될 수 있다는 것을 보여준다. I(N)의 값은 AB단자를 통해 흐르는 단락 회로의 전류와 같다. 이것은 A와 B의 두단 자를 단락 시킨 후 A에서 B로 흐르는 전류를 말한다 R(N)의 값은 개방 단자 A와 B에서 반대편으로 바라본 저항이다. R(N)을 구할 때 개방 단자들은 테브낭 정리에서 R(TH)를 계산할 때처럼 단락 시키지 않고 개방한 상태로 둔다. 실제로 이 저항은 노턴 등가 회로와 등가 회로에서 동일한 값을 가진다 노턴 회로인 경우에 R(AB)의 값은 전류원과 병렬인 R(N)과 같고 테브낭의 경우엔 전압원과 직렬 R(TH)와 같다.
회로의 노턴화
이에 대한 예로 서 아래 회로 그림에서 전류 I(L)을 다시 계산해보자.
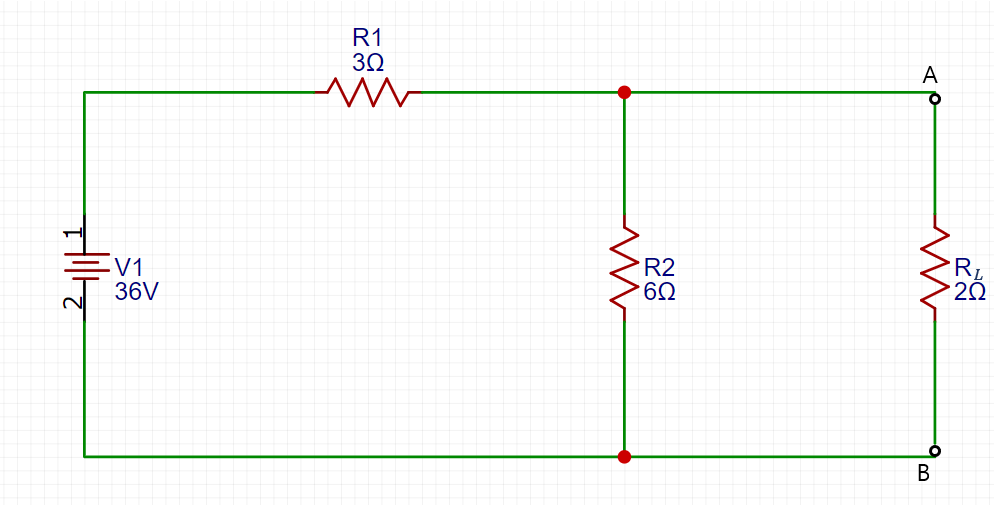
이 회로는 테브낭 정리를 적용하여 전의 포스트에서 해석했었다. 노턴 정리를 적용하는 첫 번째 단계는 아래 회로 그림과 같이 단자 A와 비 사이를 단락 회로로 생각하는 것이다. 얼마만큼의 전류가 단락 회로에 흐를까 AB를 단락 시키면 R(L)와 함께 병렬인 R2도 단락 된다는 것을 명심해야 한다
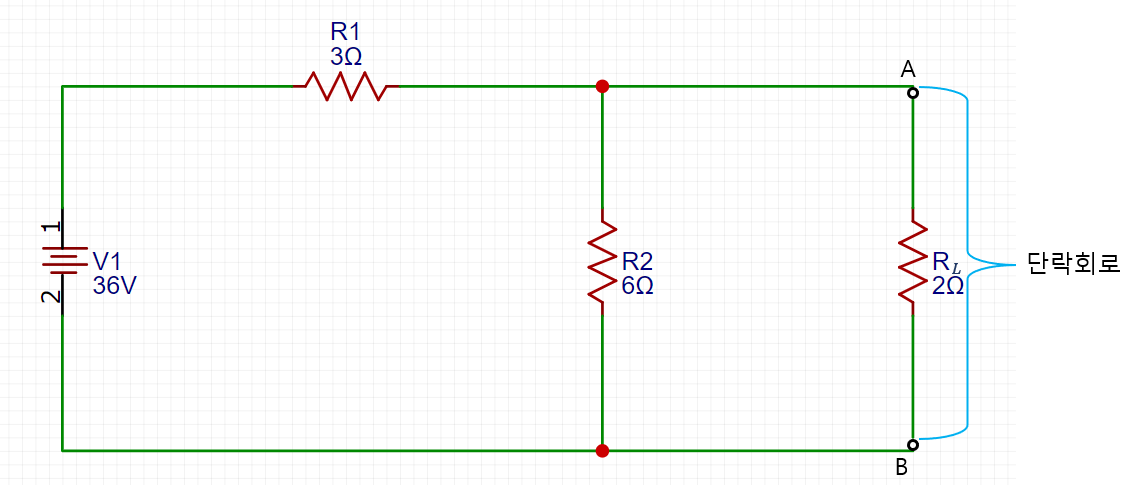
그러면 남은 유일한 저항은 회로의 남은 저항을 아래 회로 그림에서 보는 바와 같이 36V의 전원에 직렬로 연결된 3Ω의 R1이다

그러므로 단락전류는
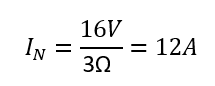
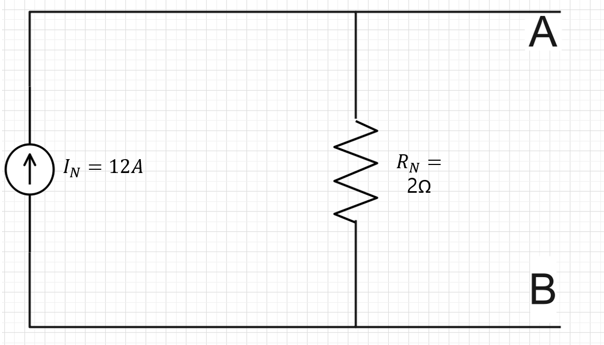
이 12A의 I(N)은 아래 회로 그림의 노턴 등가 회로에서 전류원으로부터 흐르는 전체 전류이다
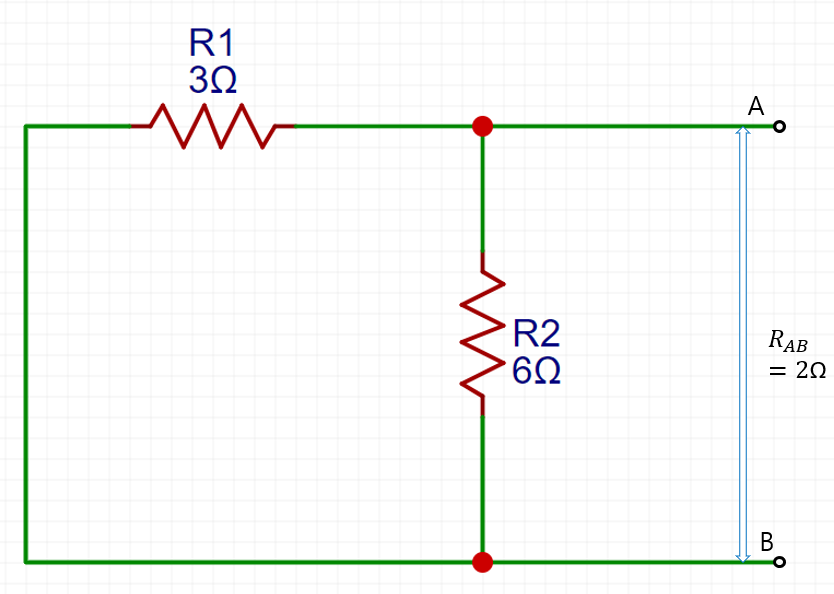
R(N)을 구하기 위해 A와 B사이의 단락을 제거하고 R(L)을 없애 단자를 개방한다. 이제 전원 V는 단락 회로로 생각해보자 아래 회로 그림에 보인 것처럼 단자 A와 B에서 바라본 저항은 3Ω과 6Ω의 병렬 저항인데 크기는 2Ω으로 R(N)과 같다.
노턴 등가 회로 최종 결과를 아래 회로 그림에 나타내었다. 노턴 등가 회로는 12A의 전류원 I(N)과 병렬인 2Ω의 R(N)으로 구성된다. 전류원의 화살표는 원래 회로와 같이 단자 A에서 B로 흐르는 전류의 방향을 보여준다. 마지막으로 I(L)을 계산하기 위해 아래 회로 그림처럼 단자 A와 B사이를 2Ω의 R(L)로 대치한다. 전류원은 여전히 12A 공급하지만 이제 그전류는 R(N)과 R(L)의 두 가지로 나누어진다. 두 저항의 크기가 같기 때문에 1A의 I(N) 각가지로 6A씩 나누어 흘러 I(L)은 6A가 된다

'공학 > 전기' 카테고리의 다른 글
| GROB's basic electronics 회로 이론-8.회로망정리(브리지회로의 테브낭화) (0) | 2022.08.10 |
|---|---|
| GROB's basic electronics 회로 이론-8.회로망정리(전압원이 2개인회로의 테브낭화) (0) | 2022.08.09 |
| GROB's basic electronics 회로 이론-8.회로망정리(테브낭정리) (0) | 2022.08.08 |
| GROB's basic electronics 회로 이론-8.회로망정리(중첩정리) (0) | 2022.08.04 |
| GROB's basic electronics 회로 이론-7.키르히호프법칙(망전류법) (0) | 2022.08.03 |